Combinations and Permutations
What's the Difference?
In English we use the word "combination" loosely, without thinking if the order of things is important. In other words:
| "My fruit salad is a combination of apples, grapes and bananas" We don't care what order the fruits are in, they could also be "bananas, grapes and apples" or "grapes, apples and bananas", its the same fruit salad. | |
| "The combination to the safe is 472". Now we do care about the order. "724" won't work, nor will "247". It has to be exactly 4-7-2. |
So, in Mathematics we use more precise language:
| When the order doesn't matter, it is a Combination. | |
| When the order does matter it is a Permutation. |
 | So, we should really call this a "Permutation Lock"! |
In other words:
A Permutation is an ordered Combination.
| To help you to remember, think "Permutation ... Position" |
Permutations
There are basically two types of permutation:
- Repetition is Allowed: such as the lock above. It could be "333".
- No Repetition: for example the first three people in a running race. You can't be first and second.
1. Permutations with Repetition
These are the easiest to calculate.
When a thing has n different types ... we have n choices each time!
For example: choosing 3 of those things, the permutations are:
n × n × n (n multiplied 3 times)
More generally: choosing r of something that has n different types, the permutations are:
n × n × ... (r times)
(In other words, there are n possibilities for the first choice, THEN there are n possibilites for the second choice, and so on, multplying each time.)
Which is easier to write down using an exponent of r:
n × n × ... (r times) = nr
So, the formula is simply:
| nr |
| where n is the number of things to choose from, and we choose r of them (Repetition allowed, order matters) |
2. Permutations without Repetition
In this case, we have to reduce the number of available choices each time.

For example, what order could 16 pool balls be in?
After choosing, say, number "14" we can't choose it again.
So, our first choice has 16 possibilites, and our next choice has 15 possibilities, then 14, 13, etc. And the total permutations are:
16 × 15 × 14 × 13 × ... = 20,922,789,888,000
But maybe we don't want to choose them all, just 3 of them, so that is only:
16 × 15 × 14 = 3,360
In other words, there are 3,360 different ways that 3 pool balls could be arranged out of 16 balls.
Without repetition our choices get reduced each time.
But how do we write that mathematically? Answer: we use the "factorial function"
 |
The factorial function (symbol: !) just means to multiply a series of descending natural numbers. Examples:
|
| Note: it is generally agreed that 0! = 1. It may seem funny that multiplying no numbers together gets us 1, but it helps simplify a lot of equations. | |
So, when we want to select all of the billiard balls the permutations are:
16! = 20,922,789,888,000
But when we want to select just 3 we don't want to multiply after 14. How do we do that? There is a neat trick: we divide by 13!
16 × 15 × 14 × 13 × 12 ...
| = 16 × 15 × 14 = 3,360 | |
13 × 12 ...
|
Do you see? 16! / 13! = 16 × 15 × 14
The formula is written:
n!(n − r)!
|
| where n is the number of things to choose from, and we choose r of them (No repetition, order matters) |
Notation
Instead of writing the whole formula, people use different notations such as these:
Combinations
There are also two types of combinations (remember the order does not matter now):
- Repetition is Allowed: such as coins in your pocket (5,5,5,10,10)
- No Repetition: such as lottery numbers (2,14,15,27,30,33)
1. Combinations with Repetition
Actually, these are the hardest to explain, so we will come back to this later.
2. Combinations without Repetition
This is how lotteries work. The numbers are drawn one at a time, and if we have the lucky numbers (no matter what order) we win!
The easiest way to explain it is to:
- assume that the order does matter (ie permutations),
- then alter it so the order does not matter.
Going back to our pool ball example, let's say we just want to know which 3 pool balls are chosen, not the order.
We already know that 3 out of 16 gave us 3,360 permutations.
But many of those are the same to us now, because we don't care what order!
For example, let us say balls 1, 2 and 3 are chosen. These are the possibilites:
| Order does matter | Order doesn't matter |
| 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 | 1 2 3 |
So, the permutations will have 6 times as many possibilites.
In fact there is an easy way to work out how many ways "1 2 3" could be placed in order, and we have already talked about it. The answer is:
3! = 3 × 2 × 1 = 6
(Another example: 4 things can be placed in 4! = 4 × 3 × 2 × 1 = 24 different ways, try it for yourself!)
So we adjust our permutations formula to reduce it by how many ways the objects could be in order (because we aren't interested in their order any more):
That formula is so important it is often just written in big parentheses like this:
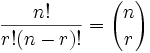 |
| where n is the number of things to choose from, and we choose r of them (No repetition, order doesn't matter) |
It is often called "n choose r" (such as "16 choose 3")
And is also known as the Binomial Coefficient.
Notation
As well as the "big parentheses", people also use these notations:
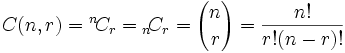
Just remember the formula:
n!r!(n − r)!
Example
So, our pool ball example (now without order) is:
| 16! | = | 16! | = | 20,922,789,888,000 | = 560 |
| 3!(16-3)! | 3!×13! | 6×6,227,020,800 |
Or we could do it this way:
| 16×15×14 | = | 3360 | = 560 |
| 3×2×1 | 6 |
It is interesting to also note how this formula is nice and symmetrical:
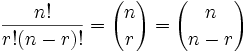
In other words choosing 3 balls out of 16, or choosing 13 balls out of 16 have the same number of combinations.
| 16! | = | 16! | = | 16! | = 560 |
| 3!(16-3)! | 13!(16-13)! | 3!×13! |
Pascal's Triangle
We can also use Pascal's Triangle to find the values. Go down to row "n" (the top row is 0), and then along "r" places and the value there is our answer. Here is an extract showing row 16:
1 14 91 364 ...
1 15 105 455 1365 ...
1 16 120 560 1820 4368 ...
1. Combinations with Repetition
OK, now we can tackle this one ...

Let us say there are five flavors of icecream: banana, chocolate, lemon, strawberry and vanilla.
We can have three scoops. How many variations will there be?
Let's use letters for the flavors: {b, c, l, s, v}. Example selections include
- {c, c, c} (3 scoops of chocolate)
- {b, l, v} (one each of banana, lemon and vanilla)
- {b, v, v} (one of banana, two of vanilla)
(And just to be clear: There are n=5 things to choose from, and we choose r=3 of them.
Order does not matter, and we can repeat!)
Order does not matter, and we can repeat!)
Now, I can't describe directly to you how to calculate this, but I can show you a special technique that lets you work it out.
Think about the ice cream being in boxes, we could say "move past the first box, then take 3 scoops, then move along 3 more boxes to the end" and we will have 3 scoops of chocolate!
So it is like we are ordering a robot to get our ice cream, but it doesn't change anything, we still get what we want.
We can write this down as  (arrow means move, circle means scoop).
(arrow means move, circle means scoop).
In fact the three examples above can be written like this:
| {c, c, c} (3 scoops of chocolate): | |
| {b, l, v} (one each of banana, lemon and vanilla): | |
| {b, v, v} (one of banana, two of vanilla): |
OK, so instead of worrying about different flavors, we have a simpler question: "how many different ways can we arrange arrows and circles?"
Notice that there are always 3 circles (3 scoops of ice cream) and 4 arrows (we need to move 4 times to go from the 1st to 5th container).
So (being general here) there are r + (n−1) positions, and we want to choose r of them to have circles.
This is like saying "we have r + (n−1) pool balls and want to choose r of them". In other words it is now like the pool balls question, but with slightly changed numbers. And we can write it like this:
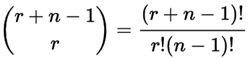 |
| where n is the number of things to choose from, and we choose r of them (Repetition allowed, order doesn't matter) |
Interestingly, we can look at the arrows instead of the circles, and say "we have r + (n−1) positions and want to choose (n−1) of them to have arrows", and the answer is the same:
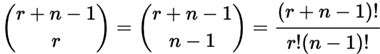
So, what about our example, what is the answer?
| (3+5−1)! | = | 7! | = | 5040 | = 35 |
| 3!(5−1)! | 3!×4! | 6×24 |
In Conclusion
Phew, that was a lot to absorb, so maybe you could read it again to be sure!
But knowing how these formulas work is only half the battle. Figuring out how to interpret a real world situation can be quite hard.
But at least now you know how to calculate all 4 variations of "Order does/does not matter" and "Repeats are/are not allowed".
QUESTION
Q.1
Jones is the Chairman of a committee. In how many ways can a committee of 5 be chosen from 10 people given that Jones must be one of them?
A
126
B
252
C
495
D
3,024
Q.2
How many permutations of 4 different letters are there, chosen from the twenty six letters of the alphabet?
A
14,950
B
23,751
C
358,800
D
456,976
Q.3
How many permutations of 3 different digits are there, chosen from the ten digits 0 to 9 inclusive?
(Such as drawing ten numbered marbles from a bag, without replacement)
(Such as drawing ten numbered marbles from a bag, without replacement)
A
84
B
120
C
504
D
720


![[image]](https://www.mathopolis.com/questions/images/3/9/cdc0f63392ea98219d4439e64998072.jpg)
![[image]](https://www.mathopolis.com/questions/images/3/5/3875114a33d55f606287386453caef2.gif)












